東大、医学部に合格する勉強法
東大・医学部受験の英語の勉強法
東大・医学部受験の数学の勉強法
東大・医学部受験の物理の勉強法
東大・医学部受験の化学の勉強法
東大・医学部受験の生物の勉強法
東大・医学部受験の現代文の勉強法
東大・医学部受験の古文・漢文の勉強法
東大・医学部受験の日本史の勉強法
東大・医学部受験の世界史の勉強法
大学入試共通テストの勉強法
英検準1級、その先へ
東大・医学部に合格する数学の勉強法:教科書+Focus Gold+合否を分ける入試問題
数学の成績が上がらずに悩んでいる人へ
どうすれば数学の成績が上がるのかがわからずに、悩んでいませんか?
実は、普段から、「なぜこうなる?」といった、物事を根本から理解しようという姿勢がある人は、今は成績が悪くても、大学受験塾チーム番町で大躍進して、東大や医学部レベルに達する可能性は高いと思います。
塾長は、数学の成績が全く足りていない人達を、何人も東大や国立医学部に導いてきました。
自分は数学のセンスが無い、と思って数学をあきらめようとしている人へ。
学校の定期テストや大学入試(東大入試まで含む)の数学というものは、むやみに難しい問題に取り組んでいれば、思考力、発想力、センスが身につき、問題を解けるようになる、というものではありません!
東大入試も、平均的な合格者は、教科書の理解し、受験によく出る技法をマスターし、知識で問題を解いているのです。そのあたりを記事にしています。
↓↓↓
2018年 東大数学(下のほう)
数学の入試問題分析
学校の定期テストや、模試の問題、解説を持って、大学受験塾チーム番町の無料学習相談に来ませんか?
テストや模試でできなかった問題の中に、大学受験塾チーム番町で使っている教材に載っているような問題が多いと思います。それは、東大や医学部の入試でも同じです。センスではなく、基本的な理解、入試によく出る技法の知識が足りていない、という考え方をオススメします。
数学ができるようにならない人:教科書読んでますか?
東大や医学部にに何十人も合格するような高校でも、数式などの意味を理解しようとせずに、ただ、問題の解き方を覚えればいい、という姿勢の人もいます。
たとえば、「関数」の定義は、中1の教科書に書いてありますが、塾長の経験上、東大に20人ほど合格する高校にも「関数って何?」と尋ねて、適切に答えられない人は、2割ほどいます。そして、数学の成績は壊滅的です。たとえば、「xを決めれば、yがただ1つ決まる」ということを理解していないので、高校の二次関数で、絶対値などがついた、少し複雑な関数になると、1つのx座標にyの値が2つあるグラフを平気で書いて疑問を持ちません。
塾長は、教科書に書いてあるような「理解」の部分をわかりやすく説明し、根本から理解できるように指導いたしますが、人間、長い年月の末、身についた習慣は変えるのが難しいこともあるようです。科学的に言うと、脳に、不適切な神経回路が形成されている、スポーツに例えると、不適切なフォームで固まってしまっている、のだと思います。
根本から理解するようになる人もいますし、そうしようとしない人もいます。
正直に告白しますと、大学受験塾チーム番町を退塾する人は、年に1人ほどはいます。それは、多くの場合、かなり早い時期から、数学を解き方の丸暗記と履き違えて、進学校の数学のテストでどうにもならなくなり、当塾に来たものの、支離滅裂な答案を書き続け、気が短い保護者の方(科学的に言って、不適切に深く形成された神経回路は、そう短期間で書き換わらないと思います)に辞めさせられる、というケースです。
塾長の経験:論理的でない人が数学を勉強すると論理的になれる?
論理的でない人は、まず、大学入試の数学で通用しません。
では、論理的でない人が、数学の学習を続けることにより、論理的になり、数学の成績も上がるのでしょうか?
塾長の経験上、論理的になれないと思います。
なぜなら、おそらく科学的には、すでに脳に「論理的でない神経回路」のようなものが構築されており、数学を「論理的でない神経回路」で処理するので、「論理的でない神経回路」が強化され続けるだけだろうからです。
したがって、論理的でない人が数学の成績を上げようと思ったら、まずは、論理に絞るのが良いかと思います。大学受験塾チーム番町では、そのように指導しております。
東大・医学部受験数学の流れ
教科書
「問題以前」の理解、基本問題
↓
Focus Gold(啓林館)
入試によく出る技法
(ここまでで、学校のテストは東大や医学部レベルの順位になり、標準的な記述模試では東大や医学部レベルの成績になると思います。東大や医学部の入試も、ほぼ、ここまでの組み合わせ、ひとひねりで十分に合格点に達します。)
↓
入試で合否を分ける問題
という流れになります。
東大、京大、国立医学部で合否を分けるレベルも、せいぜいこの組み合わせ、ひとひねりです。平均的な合格者はこれ以上の問題は解けません。
東大・医学部数学で合格点を取るには?
大学入試の数学は、同じ年の同じ大学の問題の中でも、難易度の波が大きいことが多いです。(それに対し、物理、化学などは、標準的な内容を網羅的にマスターすれば、満点近く取れることも多いです。)平均的な合格者は、単に、簡単な問題から順番に取れていて、難しい問題はできない、という場合がほとんどです。
『月刊大学への数学』の東京出版が出している参考書は、難易度をA~Dに分類しています。Bは入試標準問題、だいたい、『Focus Gold』(啓林館)などに載っている入試によく出る技法の組み合わせ、ひとひねりで解け、「思考力」「発想力」といったものは不要です。
東大は入試の成績開示をしており、かつて東大新聞は合格者の平均点を調査していました。東大理系は、Bを完答、CでBレベルの部分点くらいで、十分合格者平均に達します。
平均的な東大合格者でも解けないような難問に取り組みつつも、合否を分ける標準レベルの内容に抜けが多く、受験に成功しない人も多いようです。気をつけましょう。
数学の教科書
大学受験塾チーム番町では、基本的な理解の部分を教科書を使って学習します。
基本的に、進学校でよく採用される、数研出版の最上位の教科書を採用しています。(教科書番号はご質問ください。)
教科書には、数学の問題以前の「理解」の部分がしっかり書かれています。教科書を「理解」すると、数学の「意味」がわかるので、下記の「受験によく出る技法」を東大、医学部レベルで合否を分ける問題について、使いこなせるようになります。
また、東大、医学部を始め、上位の大学ほど、参考書にそのまま載っているような有名問題というよりは、初めて見るような問題だけど、問題文を読み取って、教科書レベルの式を立てていけば解ける、といった問題を出題することが多いです。
教科書レベルの内容を組み合わせて作ることができる問題の数は、おそらく無限に近いので、予備校の授業などで解説を受けた問題でカバーするのは無理です。
いちばん大切なのは教科書なのです。
まずは、教科書の説明を理解し、本文(章末除く)の問題を全問解けるようにしましょう。
大学受験塾チーム番町は個別指導塾なので、問題以前の「理解」の部分の解説を受け、基本例題の解説をうけ、基本問題を解くことができます。
復習の方法は、問題は、勉強法の基本の(2)単語、短答ではない問題型へ。用語や公式は(3)単語カード型がいいでしょう。
東大・医学部受験数学によく出る技法
大学受験塾チーム番町では、教科書を超えた、受験によく出る技法の学習に『Focus Gold』(啓林館)を採用しています。当塾は個別指導塾なので、塾長が例題を解説し、生徒が実際に問題を解くことができます。教科書→入試の壁を簡単に超えることができ、生徒を東大レベルの、まあ、一歩手前くらいまでは連れて行くことができます。
(Amazonには在庫がないため定価より高い可能性があります)
東大、医学部入試まで含めて、合否を分けるのは『Focus Gold』の本文の問題の、組み合わせ、ひとひねりレベルです。
学校の定期テストでは、大学受験塾チーム番町で扱った問題を全問解けるようにすれば、校内の東大、医学部合格レベルの順位に入れると思います。進研模試、河合全統記述模試など、標準レベルの記述模試では、ここまでで東大、医学部級の成績に達すると思います。
復習の方法は、勉強法の基本の(2)単語、短答ではない問題型へ。
数学の場合、思い出せなくても、5分ほどは考えたほうが、記憶の定着が良いのではないか、と昔から言われます。また、毎回、実際に手を動かして解くのか、方針が思い浮かべばOKとするかは、自分の状況を考えて決めましょう。毎回手を動かすと、復習の回転数が足りず、受験に必要なことを定着させられない可能性が出てくると思います。
東大・医学部受験で合否を分けるレベルの入試問題演習
『Focus Gold』で学んだ技法を入試問題で使いこなすため、また、完答する問題と部分点狙いの問題を見抜くため、過去問などを使って実戦問題演習をします。
多くの大学の入試問題の難易度について、上記の東京出版の本で、第三者の評価を知ることができます。
復習の方法は、勉強法の基本の(2)単語、短答ではない問題型へ。
整数問題は、東大、国立医学部でよく出題されますが、いい市販の教材がないので、塾長が各大学の過去問から厳選した問題集を配布しております。
合格る確率(文英堂)
確率は東大、医学部入試でよく出題される分野ですが、Focus Goldやチャート式では対策が弱い分野です。
大学受験塾チーム番町では、本書を採用しています。東大、上位国立医学部入試にかなり近いところまで対応しています。
この問題が合否を決める!(東京出版)
毎年、今年の入試で合否を分けたこの1題(東京出版)という本が出ています。その年の各大学の問題で、合否を分けたと思われる問題を1題取り上げています。その中から、3年分から選りすぐったものが、本書です。
東大、国立医学部で、どの辺りのレベルで合否が分かれているのかを体感できますし、実際に、合否を分ける問題の演習をできるので、意義のある本かと思います。
ただ、東京出版の本なので、解説は親切ではないです。
理系数学良問のプラチカ1A2BC
半分ほどは、Focus Gold本文の問題と重複しています。
進研記述模試や河合全統記述模試など、標準的な記述模試で、東大、国立医学部の偏差値に近づいたら、Focus Goldの網羅を続けつつ、使ってもいいでしょう。
ちなみに、理系プラチカ数3は、東大合格レベルを超えている難しい教材なので、気をつけましょう。
文系数学良問のプラチカ1A2BC
「文系」とありますが、上記の「理系プラチカ」より難易度が高く、ほぼ東大、上位国立医学部レベルと言えます。
進研記述模試や河合全統記述模試など、標準的な記述模試で、東大、上位国立医学部の偏差値あたりになったら、使ってもいいでしょう。
ハイレベル数学完全攻略
東大、上位国立医学部合格レベル~東大入試の難しい問題で部分点狙いに行く本だと思います。
収録問題は40題ほどですが、解説の中に、その問題に関連する例題があったりします。解説はかなりいいと思います。
進研記述模試や河合全統記述模試など、標準的な記述模試で、東大の偏差値あたりを取るのはアタリマエになり、文系プラチカを終えたら、使ってもいいでしょう。
共通テストの数学の勉強法
共通テストの数学は、マーク式ゆえの独特の誘導形式が特徴です。
また、原理、本質的な事柄がマーク式で問われたり、日常生活と絡めて出題されたり、ということが挙げられます。問題の解き方を丸暗記するのではなく、学校の授業と並行して、教科書の説明を理解することが望ましいです。
二次、私大とは、かなり傾向が異なります。得意な人でも、かならず対策をしましょう。
詳しくは
をご覧ください。
大学入試の数学に思考力、発想力は必要?
大学受験の数学に、思考力、発想力は必要なのでしょうか?
また、大学受験の数学を勉強することによって、社会貢献に役立つような、思考力、発想力といったものを鍛えることはできるのでしょうか。
まず、思考力、発想力が必要かについて。
東大理Ⅲまで含めて、不要だと考えます。
まず、東大理系は150分の試験時間で大問が6問出題されます。1問あたり25分です。論述式なので、答案を書くにも、それなりの時間が必要です。1問あたり25分で「思考力、発想力」をはたして問うているでしょうか。
また、「数学で合格点を取るには?」でも書きましたが、東大新聞調べの数学の合格者平均点を見ると、平均的な東大合格者は、せいぜい、「問題文を読んで淡々と教科書レベルの式を立てて解いていく」、「チャート式やFocus Goldあたりに載っている入試によく出る技法が使える」ような問題しか解けていないことがわかります。
ただし、東大などは、「教科書レベルの式を立てて解いていく」「チャート式やFocus Goldあたりに載っている入試によく出る技法が使える」にせよ、見た目、初めて見るような問題をよく出題します。
必要なのは、見た目が違っても同じようにやればできる、と思えるための「根本からの理解」だと思います。
次に、社会貢献に役立つような「思考力」「発想力」を鍛えることができるかについて。
極端な話をすると、小学生に微分積分の話をしても、あまりにもわからなさすぎて、頭が働いているとは思えませんね。したがって、「思考力」「発想力」を鍛えるためには、その人にとって適切なレベルであることが必要であると考えます。
まず、教科書に書いてあることは、偉大な先人の築いた体系ですから、基本的には受け入れるしかありません。
ただし、指導者がうまくヒントを出せば、公式などは高校生が自分で導けるような場面もあるとは思いますし、教科書本文に載っているちょっとした問題や章末問題などは、基本を理解したら、自分で考えて解ける場合もあるでしょう。
また、鵜呑みにするのではなく、いわゆる批判的思考、といったものは大切だと思います。
このあたりを通して、思考力、発想力を鍛えることはできるかもしれません。
次に、チャート式やFocus Goldなどの、教科書を超える問題集のレベルについて。
教科書を理解すれば、自力で解ける問題もありますが、平均的な東大合格者レベルでは、自力で解くのは難しいことも多いと思います。むしろ、塾長の経験上、このレベルを自分で解くことを求めると、「自力では解けない。自分は数学の才能がない。」と、数学を敬遠する原因になっていることも多いようです。
チャート式、Focus Goldのレベルも、基本的にはインプットすることになります。チャート式、Focus Goldなどで入試によく出る技法をマスターし、根本から理解して使いこなせるようにすると、(まだ少し抜けはありますが)東大入試あたりで完答しなければいけない問題、上記『大学への数学』誌のBレベル問題を解くことができます。この過程で、「思考力」「試行錯誤する力」などを身につけることはできそうです。ただし、「発想力」は必要ありません。
ここまでの力をつけた上で、『大学への数学』誌のCレベル問題を完答しようとする、あるいは、『大学への数学』誌の学力コンテストや数学オリンピックの問題に取り組む、などをすると、「発想力」も養成できるかもしれませんが、今まで述べてきたように、東大合格レベルより上の話です。
そもそも、東大合格レベルより上の高校数学の「発想力」を鍛えたとして、それが社会貢献につながるのでしょうか?
理学部数学科で数学の最先端を切り開きたい、と思っている人や、理論物理学者になりたい、と思っている人も、「発想力」のトレーニングの題材として、大学受験の数学の勉強が適切かは疑問です。
その他大勢の人もなおさら、他分野で「発想力」を発揮するためのトレーニングの素材が、大学受験の数学が適切かは疑問ではないでしょうか。
東大、医学部受験数学まとめ
冒頭で「合否を分ける問題の見分けかた」を書きました。世の中には、平均的な東大合格者は解けていないであろう問題を扱う参考書、予備校の授業が存在しますが、その存在意義はどこにあるのでしょうか。そのような問題に取り組んでいる受験生は、まず、数学は合格レベルにあるのでしょうか。数学でそのレベルで全く別の発想が必要な問題が出題されたとき、解けるのでしょうか。他の教科は合格レベルにあるのでしょうか。十分な合格レベルにあるならば、大学の勉強をしたほうが、建設的ではないでしょうか。
そんなことを考えます。
東大、医学部入試数学の分析
理数系が苦手な人についての新井紀子教授の研究と塾長の経験
2019年に『AIに負けない子どもを育てる』という本が何十万部も売れました。著者は著者は、数学者で国立情報学研究所社会共有知研究センター長・教授の新井紀子先生です。
新井紀子先生は「リーディングスキルテスト」(RST)を開発し、のべ18万人のデータを取っています。RSTは以下の内容を問います。
(1)文の主語、述語、目的語などを把握する力
(2)指示代名詞を把握する、省略された主語や目的語を把握する力
(3)2文の意味が同一であるか正しく判定する力
(4)小6までに習う知識と常識を動員して文の意味を理解、推論する力
(5)文章を図やグラフと比べて、内容が一致しているかを認識する力
(6)言葉の定義を読んでそれと合致する具体例を認識する能力
RSTの点数と、入学できる高校、大学の偏差値は、かなりの相関関係があるようです。
『AIに負けない子どもを育てる』では、「理数系が苦手な人は、(4)~(6)の点数が低い」としています。MARCH文系あたりにも少なからずいる、とのことです。
塾長の経験上も、高校あたりで数学ができない人は、(6)の「言葉の定義」をおろそかにして、解き方を丸暗記してきたような人が多いと思います。たとえば、「関数」の定義は中1の教科書に載っており、一次関数、二次関数と習いますが、東大に何十人も受かる高校にも、「関数って何?」と尋ねられて、適切に答えられない人は、それなりの割合でいます。そして、数学の成績は非常に悪いです。
数学学習のよくある間違い
教科書の説明を読まないで問題の解き方を丸暗記する
冒頭でも書きましたが、教科書には、問題以前の「理解」の部分がきちんと書かれています。これを読まずして。問題集に取り組んでいる人が、世の中には多いと思います。ですが、これは「解き方の丸暗記」で、まず、上位大学では、丸暗記では追いつかず、通用しないでしょう。
自分の実力に合わない教材を使う
特に、大学受験数学の場合、「簡単すぎるものをやっている」という失敗は少なく、「難しすぎるものをやっている」ことによる失敗が多いと思います。たとえば、教科書本文の問題をろくにマスターしていないのに、Focus Goldに取り組む、Focus Goldをろくにマスターしておらず、模試の成績もたりないのに、塾、予備校で、東大合格者も解けないような問題の解説講義を受ける、などです。
教材のマスターの目安は、9割以上、だと思います。まあ、数学の教科書本文の問題は、最終的には全問解けなければいけないのですが、人生、ある程度の見切り発車も必要で、そう考えると9割、という数字になるかと思います。
教材を「マスター」しようとしていない
上記のように、教科書は最終的には全問、Focus Goldは当塾指定の問題は、まあ9割以上解ける、状態が必要です。
ただ、世の中には、教材に書いてあることをマスターすることを目的としていなかったり、また「何周」などと復習の重要性が広まってきたことはいいことだと思いますが、方法が適切ではなかったり(1周する前に、もっと復習をたくさん入れるべきです)することが多いです。
「数学のセンス」などといったものより、このようなことで数学の成績が決まっている部分も多いです。気をつけましょう。
数学の証明が苦手な人へ:論理的思考を養うためのポイント
数学で証明が苦手な人は多いと思います。
厳しいことを言うと、論理的でない人は、自分が論理的でないことに自覚がないので、自分が論理的でない答案を書いていることに、自覚すらない場合が多いです。東大に何十人受かる高校にも、このような人は、それなりの割合でいます。
数学の証明とは?
中2の数学の教科書に、証明はどうすればよいかが書いてあります。おおむね
「仮定から出発して、すでに正しいことが明らかにされた事柄を根拠に、結論を導けば良い。」
といったことが書いてあると思います。
「仮定」と「結論」とは
数学の問題では
○○○ ならば △△△
の形で述べられることがあります。この時、○○○を「仮定」、△△△を「結論」と言います。
証明のありがちな間違い
上記の証明の手順
「仮定から出発して、すでに正しいことが明らかにされた事柄を根拠に、結論を導けば良い。」
をわかりやすく言い換えると、こうなるでしょう。
「仮定と今まで習ったことを使い、結論を導く。」
では、実際に、簡単な証明問題をやってみましょう。
問
下図の四角形OPQRにおいて、
OP=OQ、PR=QR(仮定)
ならば
∠POR=∠QOR(結論)
であることを証明せよ。
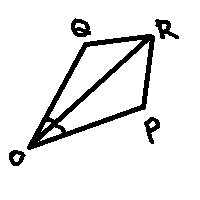 」
」
証明
仮定より OP=OQ…①、PR=QR…②
また OR=OR(共通)…③
①、②、③より、3組の辺がそれぞれ等しいから
△OPR≡△OQR (すでに習ったこと)
合同な図形では対応する角は等しいから(すでに習ったこと)
∠POR=∠QOR(結論) (証明終わり)
こんな感じです。
ところが、東大に何十人受かる高校にも、いきなり
「条件より∠POR=∠QOR」
といった、いきなり証明すべき結論を、正しいものとして答案中に書くような人が、それなりの割合でいます。
おそらく、教科書をよく読まない、論理を意識しない、などの勉強で、中学入試、高校入試を、解き方の丸覚えで乗り切ってきたのだろうと思います。
このような人は、大学入試までに数学ができなくなります。
日頃から、数学の教科書の説明の部分をよく読む、「なぜ?」「それってそもそもなに?」と疑問を持つ、などを心がけましょう。
数学のための論理を鍛える:パズルや詰将棋で考える力を磨こう!
私見の要約
2,500年前に孔子が「学びて思わざれば則(すなわ)ち罔し(くらし)、思いて学ばざれば則ち殆し(あやうし)」(『論語』)と言いました。結局、勉強しても考えなければ身につかない。考えても勉強しなければ独りよがりになる。ということだと思います。
ただし、「考える」にはどうすればいいのかは、難しい問題です。
学校は考える場ではない?
東大の哲学系の梶谷真司教授の著書『考えるとはどういうことか』(幻冬舎新書)がAmazonプライム会員はKindle版が無料だったので読んでみました。期待した内容ではありませんでしたが、
「問いかけが大切」 (一般的には、なぜ?、そもそもそれって何?、など)
とは、よく言われますが、本書のテーマだったようです。1つ、この本に、
「学校は考える場ではない」
という趣旨のことが書いてありました。私も常々、「学校の勉強は「考え」ない」と思っていました。ただし、普段から「考える」人のほうが、成績が良いという、やっかいな場所です。
たとえば、「考える」代表科目と思われがちな、数学を見てみましょう。
数学の教科書に書いてあることは、先人が築いた体系なので、受け入れるしかありません。ここで、力量のある指導者なら、公式などを導く時に、少し、生徒に考えさせることができるかもしれません。
数学の教科書に載っている問題は、先人が築いた体系を「理解」していれば、すぐ解けるもので、「考える」ことを必要としません。ただし、理解せず、解き方を丸暗記する人もいます。
それなりの進学校では、教科書の問題を超えた問題集が配られます。この問題集の問題もほぼ
(1)教科書を「理解」していればすぐ解ける
(2)段階の飛躍が大きく、並の東大合格者くらいでは、教科書を理解しただけでは解けない
に二分されます。「考え」て解ける問題は、とても少ないと思います。この「(2)型の問題が初見で解けない」という相談をよく受けます。私は上記のように「並の東大合格者くらいでは解けないよ」と答えます。当塾では例題と類題が対応した、いわゆる『チャート式』のような教材を使って解説した上で(2)型の問題に取り組んでいます。
高校の数学の先生も、ほとんどは高校時代、(2)型の問題を自力で解けなかったはずです。しかし、自分ができなかったことを生徒に「考えろ」と言う程度が、多くの場合、学校での「考える」かと思います。
むしろ、丸暗記と思われがちな歴史科などのほうが、実はA説、B説…とあったりして(たとえば、2017年のNHK大河ドラマは『おんな城主直虎』でしたが、実際は、井伊直虎が女性か男性か、から議論があります。)、本当は「考える」素材になりそうです。東大入試の日本史は、資料を与えて、高校日本史のごく基本知識から資料を読み取らせるような、実際の歴史学に近いような出題がほとんどです。
一度、論理的でない脳の回路が構築されると修正が大変
世界陸上400mハードルで2回銅メダルを獲った為末大さんは、「走る哲学者」と言われます。Googleで「為末大 早すぎる最適化」と検索すると、いくつか記事が出てきます。
記事は、「幼少期に、その体型に最適化した動きに固めると、後年体型が変わった時、過去に最適化した動きが成長を阻害する」という内容です。
先ほど、「理解せず、解き方を丸暗記する人もいます」と書きました。私に言わせれば、最適化ですらありませんが、目先の宿題、テスト、中学入試、高校入試を乗り切るには手っ取り早いかもしれません。そして、このようなタイプのほとんどが、大学入試までに数学ができなくなります。東大に何十人合格する高校にも、このような人は、それなりの割合でいます。塾長が教えても、どうしても数学ができるようにならないのが「いくら根本から教えても、丸暗記型から抜け出す気がない」タイプです。人間教育の問題もあるでしょうし、「早すぎる最適化」と同じで、解き方を丸暗記するような非論理的な神経回路が脳に強固に形成されてしまっていることもあるでしょう。
「考える」「論理的」な脳に矯正するために
先述の「なぜ?、なに?」に加え、現在は、「考えた上で正解が出る、トレーニング強度が適切な、パズルのようなもの」が良いのではないかと考えています。
(1)宮本算数教室のパズル
中学受験で有名な宮本哲也先生のパズルです。さまざまなレベルのものが(特に大書店では)売っています。いわゆる「数独」のようなものですが、四則演算が入るのが特徴的です。
(2)詰(つめ)将棋
詰将棋とは、将棋の最終盤の図面を切り取って、相手の王様を、王手、王手の連続で詰ませるパズルです。藤井聡太二冠は、小6の時、プロ棋士も参加する詰将棋解答選手権で優勝しています。(将棋は四段からプロ棋士ですが、藤井二冠はすでにプロ養成機関の二段だったようです。)書店で、1手詰という、1手だけ考えればいいものから売っていると思います。
江戸時代の名人(江戸幕府の制度)は、将軍に詰将棋を献上することになっていました。現在のタイトルとしての名人位を史上最年長の50歳で保持していた故米長邦雄永世棋聖(元日本将棋連盟会長、都教育委員)は、若手に「江戸時代の詰将棋を200題解けば、プロになれる」と言っていました。囲碁(当塾は日本棋院から100mちょっとです)の最年長タイトルホルダーの故藤沢秀行名誉棋聖は、米長永世棋聖との対談本で「それはそうでしょう」と答えています。若き日の羽生善治永世七冠も、その影響で江戸時代の詰将棋に取り組んだそうです。1つ「成績が落ちない勉強法」のコツがあるような気がします。
ただ、将棋の駒の動かし方を覚える、というハードルの高さは少しあります。
この記事を書いた人
大学受験塾チーム番町代表。東大卒。
指導した塾生の進学先は、東大、京大、国立医学部など。
指導した塾生の大学卒業後の進路は、医師、国家公務員総合職(キャリア官僚)、研究者など。学会(日本解剖学会、セラミックス協会など)でアカデミックな賞を受賞した人も複数おります。
40人クラスの33位での入塾から、東大模試全国14位になった塾生もいました。
大学受験塾チーム番町
東大、医学部に合格する勉強法
東大・医学部受験の英語の勉強法
東大・医学部受験の数学の勉強法
東大・医学部受験の物理の勉強法
東大・医学部受験の化学の勉強法
東大・医学部受験の生物の勉強法
東大・医学部受験の現代文の勉強法
東大・医学部受験の古文・漢文の勉強法
東大・医学部受験の日本史の勉強法
東大・医学部受験の世界史の勉強法
大学入試共通テストの勉強法
英検準1級、その先へ










